[Ngopini] Menghitung Peluang Mendapatkan Waifu dalam Mobage Berbasis Gacha dengan Distribusi Binomial (Studi Kasus: Kosuke Inukai dari Rikekoi)

“Oh, itu adalah kesalahpahaman yang sudah umum terjadi. Peluang 1% membuat orang-orang berpikir bahwa dengan mencoba 100 kali, mereka pasti akan mendapatkan hasil yang mereka inginkan.”

-Ena Ibarada-

CATATAN

Tulisan gabut ini sebenarnya adalah ide dari Akihisa Yoshii. Namun, karena akunnya terkena penjara selama 30 hari oleh Sang Penguasa Facebook, saya yang menggantikannya untuk menulis ini. Tulisan ini dibuat untuk mempromosikan anime Rikei ga Koi ni Ochita no de Shoumei Shitemita (biasanya disingkat sebagai Rikekoi), yang saat ini musim keduanya sudah mengudara sebanyak 3 episode.

LATAR BELAKANG

Sekarang ini, mobage (permainan genggam, biasanya digunakaan untuk permainan daring) berbasis gashapon sudah bukan hal asing dalam dunia per-otaku-an. Gashapon, biasa disingkat sebagai gacha, adalah mesin penjual otomatis yang isinya adalah kapsul berisi mainan. Cara kerjanya cukup sederhana: masukkan koin (bisa berupa uang koin maupun koin yang ditukar dengan uang) ke dalam mesinnya, putar knop pada mesinnya, dan mesin akan mengeluarkan kapsul yang berisi mainan tertentu. Pemain gacha tidak dapat memilih sendiri mainan yang mereka dapatkan. Oleh sebab itu, gacha mengharuskan pemainnya untuk mengandalkan keberuntungan untuk mendapatkan mainan yang diinginkan. Jika beruntung, mereka bisa mendapatkan mainan yang diinginkan dalam sekali coba, tetapi jika sebaliknya, maka mereka harus mencoba berulang kali untuk mendapatkan mainan yang diinginkan.

Pada tahun 2010-an, sistem gacha yang berbasis keberuntungan ini diterapkan pada mobage, sehingga para pemain mobage harus menarik gacha untuk menadapatkan barang dalam mobage yang diinginkan (misalnya karakter, senjata, dll). Ditambah dengan pengaruh moe yang sangat kuat di kalangan para otaku, merekatakkan segan menghabiskan banyak uang atau tenaga (bagi yang bermain secara gratis) demi mendapatkan waifu (karakter moe yang dianggap sebagai istri) mereka meskipun mereka tahu bahwa keberhasilan dalam “membawa pulang” waifu mereka sangat dipengaruhi oleh keberuntungan.

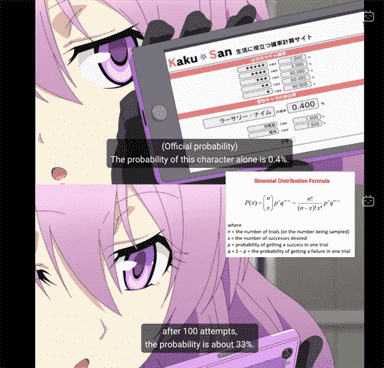
Fenomena ini dapat dilihat pada salah satu karakter dalam anime Rikei ga Koi ni Ochita no de Shoumei Shitemita, yakni Kosuke Inukai, yang dalam Season 2 Episode 3 terlihat dibuat stres oleh suatu mobage karena ia sangat ingin mendapatkan waifu-nya yang bernama Rarsaly di dalam mobage tersebut. Hal ini cukup wajar karena Rarsaly adalah karakter yang termasuk dalam limited gacha (gacha terbatas), sehingga waktu untuk mendapatkannya sangat terbatas. Jika Kosuke tidak mendapatkannya pada periode yang terbatas tersebut, siapa yang tahu kapan ia akan mendapatkan kesempatan untuk mendapatkannya lagi?

Salah satu rekan satu laboratorium Kosuke yang beberapa kali melihatnya histeris karena hasil gacha yang mengecewakan, Ena Ibarada, menyadari bahwa Kosuke salah paham terhadap peluangnya mendapatkan Rarsaly. Kesalahpahaman apa yang dilakukan oleh Kosuke? Bagaimana seharusnya Kosuke, maupun kita semua, memahami peluang mendapatkan waifu dalam mobage berbasis gacha?

SISTEMATIKA PENULISAN

Tulisan ini dibuat dengan susunan sebagai berikut:

1. Memaparkan kesalahpahaman yang dialami oleh Kosuke menurut Ena,
2. Menelusuri beberapa perbedaan antara gacha tradisional dan gacha elektronik yang dapat diamati,
3. Memperkenalkan Teori Peluang sebagai solusi untuk menyelesaikan masalah ini,
4. Mendalami kesalahpahaman Kosuke lebih jauh,
5. Memberikan asumsi untuk memodelkan usaha mendapatkan waifu dalam mobage berbasis gacha,
6. Merancang pemodelan usaha mendapatkan waifu dalam mobage berbasis gacha dengan Distribusi Binomial,
7. Melakukan kalkulasi Peluang Kosuke untuk mendapatkan Rarsaly dalam 100 kali tarikan gacha,
8. Merumuskan final model dari usaha mendapatkan waifu dalam mobage berbasis gacha,
9. Menarik kesimpulan.

KESALAHPAHAMAN KOSUKE

Dalam mobage yang dimainkan oleh Kosuke, peluang untuk mendapatkan Rarsaly dari tarikan gacha adalah 1% (setara dengan 1/100 dalam pecahan biasa), sehingga ia menganggap bahwa dalam 100 tarikan, ia pasti akan mendapatkan Rarsaly. Namun, Ena membantah klaim Kosuke dan menganggapnya sebagai kesalahpahaman umum yang dialami banyak orang.

GACHA TRADISIONAL VS GACHA ELEKTRONIK

Untuk lebih memahami kesalahpahaman Kosuke, kita perlu melihat beberapa perbedaan yang dapat diamati dari gacha tradisional (dalam mesin gacha) dan gacha elektronik (dalam mobage).

Salah satu perbedaan yang dapat diamati adalah gachatradisional yang dibatasi oleh ruang fisik (yakni dalam mesin gacha) sehingga:

• Banyak barang yang dapat ditampung dalam mesin gacha terbatas (dengan asumsi bahwa pengisian ulang hanya dapat dilakukan secara hingga). Akibatnya, banyak penarikan yang dapat dilakukan pun terbatas.
• Banyak barang dalam mesin gacha berkurang setiap dilakukan penarikan. Akibatnya, peluang mendapatkan barang yang diingikan dari mesin gacha bisa meningkat secara signifikan (sebagai akibat berkurangnya barang dalam mesin) maupun menurun secara signifikan (sebagai akibat dari kemungkinan barang yang diinginkan sudah didapatkan oleh orang lain yang sebelumnya memainkan mesin gacha tersebut).

Ruang dalam gacha elektronik tidak terbatas secara fisik oleh mesin gacha. Maka, tidak seperti pada gacha tradisional, dalam gacha elektronik, banyak barang yang dapat ditampung dalam mesin virtual gacha dapat dianggap tak hingga, dan banyak barang (maupun proporsi) setelah penarikan gacha tidak berkurang.

STATISTIKA DAN TEORI PELUANG

Dalam kehidupan ini, kita dituntut untuk memahami fenomena-fenomena yang terjadi di sekitar kita, baik fenomena alam maupun sosial. Terdapat beberapa cara untuk memahami berbagai fenomena dalam kehidupan kita. Salah satunya adalah menyajikan hasil pengamatan kita dalam bentuk data, yang kemudian dapat kita olah secara kuantitatif untuk mendapatkan deskripsi maupun menyimpulkan sesuatu dari fenomena yang kita amati dalam bentuk terukur. Statistika adalah ilmu yang membantu kita dalam mengolah data yang kita miliki.

Salah satu informasi yang dapat kita peroleh dari data adalah frekuensi (banyaknya) kemunculan masing-masing nilai/kejadian dalam suatu data. Dari frekuensi kemunculan nilai-nilai/kejadian-kejadian tersebut, kita memperoleh distribusi frekuensi, salah satu cara kita menyajikan data. Teori Peluang adalah ilmu yang membantu kita dalam memodelkan distribusi frekuensi tersebut secara teoretis-matematis.

Misalkan, kita ingin mengamati fenomena pelemparan sebuah dadu 6 mata yang seimbang. Kejadian paling sederhana yang mungkin terjadi dalam fenomena tersebut adalah kemunculan mata dadu 1, 2, 3, 4, 5, dan 6. Karena dadunya seimbang, secara teoretis kita dapat mengatakan bahwa peluang munculnya masing-masing mata dadu adalah 1/6. Frekuensi kemunculan kejadian-kejadian sederhana dalam fenomena pelemparan dadu 6 mata seimbang membentuk suatu distribusi yang bernama distribusi seragam (uniform distribution). Teori Peluang mempelajari berbagai jenis distribusi tersebut.

KLARIFIKASI KESALAHPAHAMAN KOSUKE

Bagi Kosuke, peluang untuk mendapatkan Rarsaly dari tarikan gacha adalah 1% (setara dengan 1/100 dalam pecahan biasa), sehingga ia menganggap bahwa dalam 100 tarikan, ia pasti akan mendapatkan Rarsaly. Mungkin Kosuke berpikir demikian karena ia memandang gacha dalam mobage seperti gacha tradisional. Asumsikan bahwa mesin gacha tradisional dalam bayangan Kosuke memuat 100 barang, dan 1 di antara 100 barang tersebut adalah Rarslay. Setelah tarikan pertama, tersisa 99 barang dalam mesin gacha tersebut sehingga peluang mendapatkan Rarsaly mehjadi 1/99. Kemudian, setelah tarikan kedua, tersisa 98 barang dalam mesin gacha tersebut sehingga peluang mendapatkan Rarsaly mehjadi 1/98. Pada akhirnya, setelah tarikan ke-99, hanya tersisa 1 barang dalam mesin gacha tersebut sehingga peluang mendapatkan Rarsaly mehjadi 1.

Namun, seperti yang Ena katakan, dalam gacha elektronik, meskipun kita telah berkali-kali melakukan penarikan gacha, banyak barang dalam mesin virtual gacha tidak akan berkurang, sehingga tidak mungkin tersisa 1 barang dalam mesin virtual gacha tersebut. Dalam Teori Peluang dan Kombinatorika, penarikan gacha tradisional adalah kejadian tanpa pengembalian barang, sedangkan penarikan gacha elektronik adalah kejadian dengan pengembalian barang. Oleh sebab itu, penarikan waifu dalam mobage berbasis gacha tidak mengikuti distribusi yang Kosuke pikirkan.

Ditambah lagi, ternyata peluang Kosuke mendapatkan Rarsaly dalam sekali gacha adalah 0.4%, bukan 1%.

ASUMSI PEMODELAN

Untuk membentuk pemodelan penarikan waifu dalam mobage berbasis gacha, diperlukan beberapa penyederhanaan dengan asumsi-asumsi sebagai berikut:

• Pemain mobage memiliki uang yang cukup untuk menarik gacha sebanyak yang mereka mau.
• Hasil yang diperoleh dari tarikan gacha dalam mobage benar-benar bersifat acak/random (bukan pseudorandom).
• Mobage yang dimainkan tidak menerapkan sistem spark (yakni jaminan untuk mengambil waifu yang diinginkan setelah beberapa kali penarikan, misalnya setelah 300 kali), pity, atau semacamnya.

RANCANGAN PEMODELAN DENGAN DISTRIBUSI BINOMIAL

Dalam Teori Peluang, setiap fenomena mengikuti distribusi yang beragam. Sebagai contoh, ada fenomena yang mengikuti distribusi seragam (pelemparan dadu seimbang). Lalu, bagaimana dengan penarikan waifu dalam mobage berbasis gacha? Fenomena tersebut mengikuti distribusi binomial

Pertama-tama, variabel dalam fenomena yang ingin diamati perlu dirumuskan agar lebih mudah dimodelkan dalam distribusi binomial, yaitu:

• Kemungkinan hasil sekali penarikan gacha: mendapatkan waifu, , lambangkan peluangnya sebagai p, dan tidak mendapatkan waifu, lambangkan peluangnya sebagai q.
• Dalam Teori Peluang, peluang tidak mendapatkan waifu dirumuskan sebagai q=1-p.
• Banyaknya penarikan gachayang dilakukan adalah dinyatakan dalam variabel n.
• Berapa kali waifu diperoleh dalam penarikan gacha dinyatakan dalam variabel x. Misalkan, Kosuke mendapatkan Rarsaly sebanyak 3 kali dalam penarikan gacha, maka x=3.
• Peluang mendapatkan waifu sebanyak x kalidalam n kali penarikandinyatakan sebagai Pr(X=x,n).

Dengan distribusi binomial, penarikan waifu dalam mobage berbasis gacha dimodelkan sebagai berikut:

• Pr(X=x,n)=(n!/((n-x)!x!))*p^x*(1-p)^(n-x) untuk x=0, 1, 2, 3, …, n
• Pr(X=x,n)=0 untuk x lain.

KALKULASI PELUANG KOSUKE MENDAPATKAN RARSALY

Pada tulisan ini, nilai yang hendak dicari adalah peluang Kosuke untuk mendapatkan Rarsaly dalam 100 kali tarikan gacha, , dengan p=0.004 (0.4%). Karena penarikan gacha dilakukan sebanyak 100 kali, untuk kalkulasi ini, n=100. Lalu, berapa nilai x-nya?

Perhatikan bahwa jika x=1, maka dalam 100 kali penarikan gacha, Kosuke mendapatkan Rarsaly sebanyak satu kali. Jika x=2, maka dalam 100 kali penarikan gacha, Kosuke mendapatkan Rarsaly sebanyak dua kali. Jika x=100, maka dalam 100 kali penarikan gacha, Kosuke mendapatkan Rarsaly sebanyak seratus kali. Jika x=0, maka dalam 100 kali penarikan gacha, Kosuke sama sekali tidak mendapatkan Rarsaly.

Maka, jika nilai yang dicari adalah peluang Kosuke untuk mendapatkan Rarsaly dalam 100 kali tarikan gacha, maka yang penting adalah Kosuke mendapatkan Rarsaly dalam 100 kali tarikan tersebut, tak peduli berapa kali ia mendapatkan Rarsaly. Setidaknya, Kosuke hanya perlu mendapatkan Rarsaly sekali dalam 100 kali tarikan, tetapi ia bisa juga mendapatkanya dua kali, tiga kali, bahkan 100 kali. Karena Kosuke perlu mendapatkan Rarsaly setidaknya sekali dalam 100 kali tarikan, makapeluang Kosuke untuk mendapatkan Rarsaly dalam 100 kali tarikan gacha kurang tepat bila dirumuskan sebagai Pr(X=1,100).

Perumusan yang lebih tepat adalah sebagai berikut:

Pr(X≥1,100)=Pr(X=1,100)+Pr(X=2,100)+…+Pr(X=100,100)

Namun, perumusan tersebut masih terkesan sangat menyulitkan, karena kita harus menghitung Pr(X=1,100) sampai Pr(X=100,100). Untuk mempermudah perhitungan, kita bisa melihat lawan dari kejadian Kosuke mendapatkan Rarsaly dalam 100 kali tarikan gacha. . Lawan dari kejadian tersebut tentu saja adalah Kosuke sama sekali tidak mendapatkan Rarsaly dalam 100 kali penarikan gacha. Dengan kata lain, x=0. Peluang Kosuke sama sekali tidak mendapatkan Rarsaly dalam 100 kali penarikan gacha dapat dirumuskan sebagai Pr(X=0,100), sehingga, dalam Teori Peluang, peluang Kosuke untuk mendapatkan Rarsaly dalam 100 kali tarikan gacha dapat dirumuskan sebagai berikut:

Pr(X≥1,100) = 1 – Pr(X=0,100)

Dengan kalkulasi:

Pr(X≥1,100) = 1 – Pr(X=0,100)

= 1 – (100!/((100-0)!0!))*(0.004)^0*(1-0.004)^(100-0)

= 1 – (100!/(100!*0!))*1*(0.996)^100

≈1 – 0.6698

= 0.3302

= 33.02%

≈33%.

Maka, seperti perhitungan yang dilakukan Ena (lihat gambar yang dilampirkan pada tulisan ini), peluang Kosuke untuk mendapatkan Rarsaly dalam 100 kali tarikan gacha sebenarnya kira-kira hanyalah 33%, sehingga Kosuke sama sekali tidak dijamin akan mendapatkan Rarsaly dalam 100 kali tarikan (kecuali jika diberlakukan sistem spark).

PEMODELAN PENARIKAN WAIFU DARI GACHA DALAM MOBAGE

Berdasarkan kalkulasi yang dilakukan untuk studi kasus Kosuke, untuk menghitung peluang seseorang untuk mendapatkan waifu-nya dalam nkali tarikan gacha, rumus yang digunakan adalah Pr(X≥1,n) yang dapat dijabarkan sebagai berikut:

Pr(X≥1,n) = 1 – Pr(X=0,n) = 1 – (n!/(n!*0!))*(1-p)^n

dengan p adalah peluang mendapatkan waifu dalam sekali tarikan (biasanya nilainya diberikan dalam mobage sebagai ratedari karakter tersebut).

KESIMPULAN

Dalam tulisan ini, dapat disimpulkan bahwa kegiatan menarik waifu dari gacha dalam mobage dapat dimodelkan dengan distribusi binomial dalam Teori Peluang. Kesalahpahaman dalam mencari peluang mendapatkan waifu dari gacha dalam mobage, seperti yang dialami Kosuke Inukai dari anime Rikei ga Koi ni Ochita no de Shoumei Shitemita,tak jarang terjadi karena banyak orang masih menganggap bahwa cara kerja gacha elektronik seperti dalam mobage sama seperti cara kerja gacha tradisional. Dengan menggunakan model yang dibuat berdasarkan distribusi binomial, peluang Kosuke mendapatkan Rarsaly, waifu-nya,dari 100 kali tarikan gacha sebenarnya hanyalah kira-kira 33%, seperti hasil yang dihitung oleh Ena Ibarada. Model yang diperoleh dalam tulisan ini dapat digunakan untuk menghitung peluang mendapatkan waifu dari n kali tarikan gacha dengan asumsi tidak diberlakukan sistem spark, pity, atau semacamnya.

Sumber: Akihisa Yoshii (Facebook)